International Journal of Mathematics and Computational Science
Articles Information
International Journal of Mathematics and Computational Science, Vol.4, No.4, Dec. 2018, Pub. Date: Oct. 9, 2018
Golden Mean and the Action of Mobius Group M
Pages: 124-127 Views: 2178 Downloads: 756
[01]
Qamar Afzal, Department of Mathematics, University of Lahore, Pakpattan, Pakistan.
[02]
Farkhanda Afzal, Department of Humanities and Basic Sciences, College of Telecommunication and Engineering, National University of Science and Technology, Islamabad, Pakistan.
Golden mean is an important feature of Aristotle’s' virtue theory consequently it is significant to understand and it should be easily applied to any problem. The abilities that surround Aristotle’s ethics are to be found within the Golden mean, which includes finding the balance among two means. The Golden mean, the Golden section and Golden ratio all the admired names for a mathematical concept which is defined as a number that is equal to its own reciprocal plus one. Suppose we have the extended complex plane and we define Möbius group which has order six and it is defined by linear functional transformations from extended complex plane to extended complex plane. In this paper we determine the existence of golden mean in the action on M real quadratic field and we give the orbit in which golden mean appears.
Golden Mean, Pisot Number, Salem Number, Orbit, Mobius Group
[01]
Aslam, M. M and M. A Zafar, 2011, Real Quadratic irrational Numbers and Modular Goup Action, Southeast Asian Bull. Math, 35 (3): 439-445.
[02]
Aslam, M. M and M. A Zafar, 2013,  Under the Action of
Under the Action of 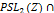
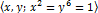 , Research Journal of Applied Sciences, Engineering and Technology, 5 (6): 1916-1922.
[03]
D. Boyd, Pisot and Salem Numbers in intervals of the real line, Math. Comp, 32 (1978), 1244–1260.
[04]
D. Boyd, Small Salem Numbers, Duke Math. J. 44 (1977), 315- 328.
[05]
F. Afzal, Q. Afzal & M. A. Malik “A Classification of the Real Quadratic irrational numbers
, Research Journal of Applied Sciences, Engineering and Technology, 5 (6): 1916-1922.
[03]
D. Boyd, Pisot and Salem Numbers in intervals of the real line, Math. Comp, 32 (1978), 1244–1260.
[04]
D. Boyd, Small Salem Numbers, Duke Math. J. 44 (1977), 315- 328.
[05]
F. Afzal, Q. Afzal & M. A. Malik “A Classification of the Real Quadratic irrational numbers  w.r.t modulo 3r”, International Mathematical Forum, Vol. 7, 2012, no. 39, 1915–1924.
[06]
F. Afzal, I. S. Bhatti & M. A. Malik “Action of G and M on
w.r.t modulo 3r”, International Mathematical Forum, Vol. 7, 2012, no. 39, 1915–1924.
[06]
F. Afzal, I. S. Bhatti & M. A. Malik “Action of G and M on  & Algorithmic Implementation of Group Actions”, Journal of Hyperstructures, Vol. 1, 2012, no. 1, 42–52.
[07]
F. Afzal, Q. Afzal & M. A. Malik “Modular Group Action on Quadratic Field by Linear congruence”, Novi Sad Journal Of Mathematics, Vol. 42, 2012, no. 2, 127–137.
[08]
F. Afzal, Q. Afzal & M. A. Malik “Quadratic Fields under the Action of Subgroup of M”, IJMO 2013 Vol. 3 (3): 283-287.
[09]
F. Afzal & Q. Afzal, “Quadratic Irrationals and Symmetries of Continued Fraction", International Journal of Mathematical Archive, Vol. 4, no. 3, 7-12, 2013.
[10]
G. Higman and Q. Mushtaq, 1983, Coset Diagrams and Relations for PSL (2, Z), Arab Gulf J. Sc, Res. 1 (1), pp 159-164.
[11]
H. H. Otto, Should we pay more attention to the relationship between the golden mean and the Archimedes’ constant? Nonlinear Sci. Lett. A, 8 (4) (2017), pp. 410-412.
[12]
H. H. Otto, Mass Constituents of a Flat Lattice Multiverse: Conclusion from Similarity between Two Universal Numbers, the Rocksalt-Type 2D Madelung Constant and the Golden Mean. Journal of Modern Physics (2018), 9, 1-13.
[13]
M Aslam Malik, S. M Husnine and Abdul Majeed, Action of the Mobius group
& Algorithmic Implementation of Group Actions”, Journal of Hyperstructures, Vol. 1, 2012, no. 1, 42–52.
[07]
F. Afzal, Q. Afzal & M. A. Malik “Modular Group Action on Quadratic Field by Linear congruence”, Novi Sad Journal Of Mathematics, Vol. 42, 2012, no. 2, 127–137.
[08]
F. Afzal, Q. Afzal & M. A. Malik “Quadratic Fields under the Action of Subgroup of M”, IJMO 2013 Vol. 3 (3): 283-287.
[09]
F. Afzal & Q. Afzal, “Quadratic Irrationals and Symmetries of Continued Fraction", International Journal of Mathematical Archive, Vol. 4, no. 3, 7-12, 2013.
[10]
G. Higman and Q. Mushtaq, 1983, Coset Diagrams and Relations for PSL (2, Z), Arab Gulf J. Sc, Res. 1 (1), pp 159-164.
[11]
H. H. Otto, Should we pay more attention to the relationship between the golden mean and the Archimedes’ constant? Nonlinear Sci. Lett. A, 8 (4) (2017), pp. 410-412.
[12]
H. H. Otto, Mass Constituents of a Flat Lattice Multiverse: Conclusion from Similarity between Two Universal Numbers, the Rocksalt-Type 2D Madelung Constant and the Golden Mean. Journal of Modern Physics (2018), 9, 1-13.
[13]
M Aslam Malik, S. M Husnine and Abdul Majeed, Action of the Mobius group 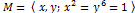 on certain real quadratic fields, PUJM, (2011), Vol. 36, pp 71-88.
[14]
M Aslam, Q Mushtaq, T Masood and M Ashiq, Real Quadratic irrational numbers and the group
on certain real quadratic fields, PUJM, (2011), Vol. 36, pp 71-88.
[14]
M Aslam, Q Mushtaq, T Masood and M Ashiq, Real Quadratic irrational numbers and the group 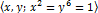 , Southeast Asian Bulletin of Mathematics, (2003), Vol. 27, pp 409-415.
[15]
Q. Mushtaq and M. Aslam, 1997, Transitive action of a two generator group on rational projective line, Southeast Asian Bulletin of Mathematics, 1, pp 203-207.
[16]
Q. Mushtaq and M. Aslam, 1998, Group Generated by Two Elements of Orders Two and six acting on R and Q(√n), Discrete Mathematics, 179, pp 145-154.
[17]
Q. Mushtaq and Arshad Mahmood, A note on Salem numbers and Golden mean, Quasigroups and Related Systems 11 (2004), 91–93.
[18]
R. Salem, Algebraic Numbers and Fourier Analysis, Wadsworth 1983.
[19]
V. Flammang, M. Grandcolas and G. Rhin, Small Salem Numbers in Number Theory in Progress, Vol. 1, de Gruyter, 1999, 165–168.
, Southeast Asian Bulletin of Mathematics, (2003), Vol. 27, pp 409-415.
[15]
Q. Mushtaq and M. Aslam, 1997, Transitive action of a two generator group on rational projective line, Southeast Asian Bulletin of Mathematics, 1, pp 203-207.
[16]
Q. Mushtaq and M. Aslam, 1998, Group Generated by Two Elements of Orders Two and six acting on R and Q(√n), Discrete Mathematics, 179, pp 145-154.
[17]
Q. Mushtaq and Arshad Mahmood, A note on Salem numbers and Golden mean, Quasigroups and Related Systems 11 (2004), 91–93.
[18]
R. Salem, Algebraic Numbers and Fourier Analysis, Wadsworth 1983.
[19]
V. Flammang, M. Grandcolas and G. Rhin, Small Salem Numbers in Number Theory in Progress, Vol. 1, de Gruyter, 1999, 165–168.

ISSN Print: 2381-7011
ISSN Online: 2381-702X
Current Issue:
Vol. 5, Issue 2, June Submit a Manuscript Join Editorial Board Join Reviewer Team
ISSN Online: 2381-702X
Current Issue:
Vol. 5, Issue 2, June Submit a Manuscript Join Editorial Board Join Reviewer Team
| About This Journal |
| All Issues |
| Open Access |
| Indexing |
| Payment Information |
| Author Guidelines |
| Review Process |
| Publication Ethics |
| Editorial Board |
| Peer Reviewers |


